## 传统方法的局限 在算法竞赛中,树状数组(Fenwick Tree)因其简洁高效的特性被广泛使用。但传统实现需要预先确定数据范围并预分配空间,当值域达到1e18量级时,离散化预处理会带来诸多不便:需要离线处理、增加编码复杂度。 ## 动态空间的黑魔法 我们可以利用unordered_map的无序容器特性配合树状数组的跳跃特性,实现动态内存分配的树状数组,创建出一个1e18甚至更大的树状数组,可以省去离散化的步骤,同时无需离线 ```cpp #define LL long long unordered_map<LL, LL> tree; const LL N = 1e18 + 10; LL lowbit(LL x) {return x & -x;} void add(LL x, LL v) { while(x <= N) { tree[x] += v; x += lowbit(x); } } LL sum(LL x) { LL sum = 0; while(x) { sum += tree[x]; x -= lowbit(x); } return sum; } ``` ## 实现原理分析 1. **空间动态分配**:unordered_map仅在访问时创建键值对,实际空间复杂度约为O(q logU),其中q是操作次数,U是值域大小 2. **时间效率折衷**:哈希表访问时间复杂度为均摊O(1),但实际常数比普通数组大,在ICPC比赛中请分析好时间再谨慎使用。 ## 优势与代价 ✅ 优势: - 对于超大值域无需预处理,支持在线操作 - 节省内存空间(稀疏数据场景) ⚠️ 注意事项: - 时间复杂度常数**较大** - 哈希冲突导致时间复杂度最坏至O(n)(可参考自定义哈希篇) ## 实战 下面是使用超大树状数组做的题 [1D Country - AtCoder abc371\_d - Virtual Judge](https://vjudge.net/problem/AtCoder-abc371_d) 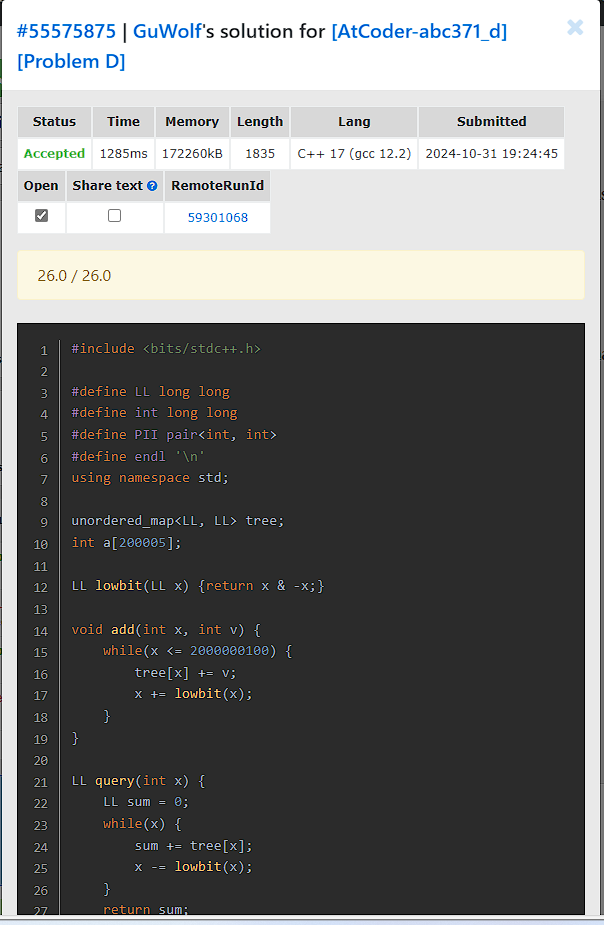 ## 使用建议 推荐在以下场景使用该技巧: 1. 值域极大但操作次数有限(q ≤ 1e5) 2. 需要快速实现原型的情况 3. 内存资源紧张的环境 Loading... ## 传统方法的局限 在算法竞赛中,树状数组(Fenwick Tree)因其简洁高效的特性被广泛使用。但传统实现需要预先确定数据范围并预分配空间,当值域达到1e18量级时,离散化预处理会带来诸多不便:需要离线处理、增加编码复杂度。 ## 动态空间的黑魔法 我们可以利用unordered_map的无序容器特性配合树状数组的跳跃特性,实现动态内存分配的树状数组,创建出一个1e18甚至更大的树状数组,可以省去离散化的步骤,同时无需离线 ```cpp #define LL long long unordered_map<LL, LL> tree; const LL N = 1e18 + 10; LL lowbit(LL x) {return x & -x;} void add(LL x, LL v) { while(x <= N) { tree[x] += v; x += lowbit(x); } } LL sum(LL x) { LL sum = 0; while(x) { sum += tree[x]; x -= lowbit(x); } return sum; } ``` ## 实现原理分析 1. **空间动态分配**:unordered_map仅在访问时创建键值对,实际空间复杂度约为O(q logU),其中q是操作次数,U是值域大小 2. **时间效率折衷**:哈希表访问时间复杂度为均摊O(1),但实际常数比普通数组大,在ICPC比赛中请分析好时间再谨慎使用。 ## 优势与代价 ✅ 优势: - 对于超大值域无需预处理,支持在线操作 - 节省内存空间(稀疏数据场景) ⚠️ 注意事项: - 时间复杂度常数**较大** - 哈希冲突导致时间复杂度最坏至O(n)(可参考自定义哈希篇) ## 实战 下面是使用超大树状数组做的题 [1D Country - AtCoder abc371\_d - Virtual Judge](https://vjudge.net/problem/AtCoder-abc371_d)  ## 使用建议 推荐在以下场景使用该技巧: 1. 值域极大但操作次数有限(q ≤ 1e5) 2. 需要快速实现原型的情况 3. 内存资源紧张的环境 最后修改:2025 年 03 月 18 日 © 允许规范转载 打赏 赞赏作者 支付宝微信 赞 如果觉得我的文章对你有用,请随意赞赏